Here is a picture of the setup of the inertial balance with 800g of mass added and the equipment recording the data from the oscillations of the balance.
PROCEDURE
A C-clamp was used to secure the balance to the table and a piece of tape was used to break the beam between the photgate. After the computer was setup, measurements of the period of the balance with different masses were taken and recorded. We started with just the balance and added 100g after each measurement until we reached our maximum mass of 800g. Below is a table of our data. As you can see, the more mass that is added, the slower the period is.
After we recorded our data, we used 2 different objects(in our case a cell phone and water bottle) and placed them on the balance and recorded their periods. We will use these periods to determine if our power law equation is accurate or not.
THE POWER-LAW EQUATION
We now have to find a relationship between mass and period using a power equation. We started off by using the base equation below and reworked it to mimick the form of an equation of the line.
We then plotted out data into a mass v. period graph in logger pro and used a line fir to provide us with our constants of the mass of the tray. We found a range of the mass of the tray which yielded us with a 0.9999 correlation between the graph and our points. We then used this range to best provide our team with a mass of our objects.
Here is the final equation which will give us our mass of our known objects of varying mass
At first, our numbers were not matching up but we then realized that we had to use an exponential in the base of the exponential and this solved our problem. The final result was an equation that yielded us an answer that was within ± .001g of the actual maass. Needless to say, this equation was very accurate.



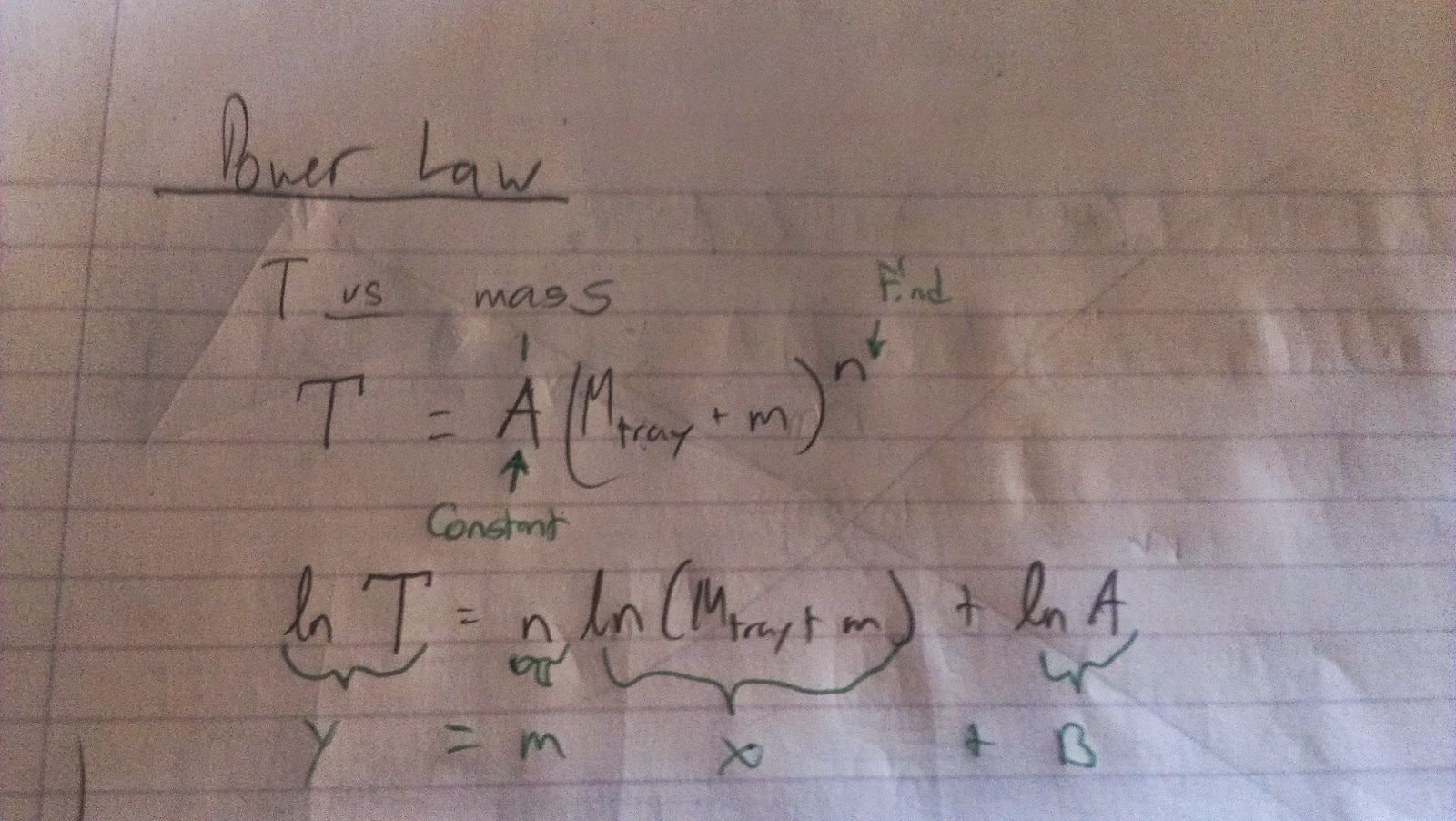



No comments:
Post a Comment